Balanced Binary Trees
A balanced binary tree or a self-balancing binary search tree is any node-based binary search tree that automatically keeps its height (maximal number of levels below the root) small in the face of arbitrary item insertions and deletions. [1]
AVL Tree
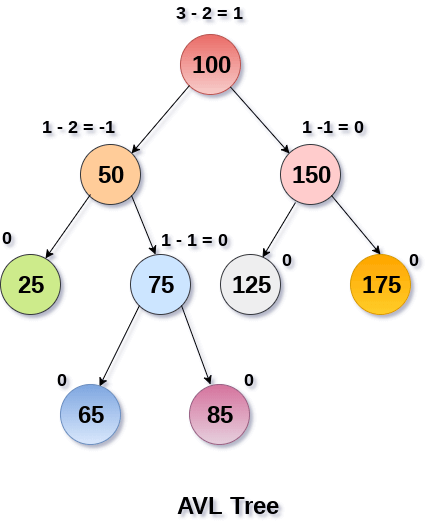 |
|---|
| AVL tree with balance factors[2] |
Height difference tolerance: 1
| Algorithm | Average | Worst case |
|---|---|---|
| Space | ||
| Search | ||
| Insert | ||
| Delete |
Implementation is derived from GeeksforGeeks
class TreeNode(object):
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
self.height = 1
class AVL_Tree(object):
@staticmethod
def search(root: TreeNode, key: int) -> TreeNode:
now = root
while now:
if now.val == key:
return now
if key < now.val:
now = now.left
if key > now.val:
now = now.right
return None
@staticmethod
def insert(root: TreeNode, key: int) -> TreeNode:
if not root:
return TreeNode(key)
elif key < root.val:
root.left = AVL_Tree.insert(root.left, key)
elif key > root.val:
root.right = AVL_Tree.insert(root.right, key)
else:
raise KeyError
root.height = 1 + max(
AVL_Tree.get_height(root.left), AVL_Tree.get_height(root.right))
balance = AVL_Tree.get_balance(root)
if balance > 1 and key < root.left.val:
return AVL_Tree._right_rotate(root)
if balance < -1 and key > root.right.val:
return AVL_Tree._left_rotate(root)
if balance > 1 and key > root.left.val:
root.left = AVL_Tree._left_rotate(root.left)
return AVL_Tree._right_rotate(root)
if balance < -1 and key < root.right.val:
root.right = AVL_Tree._right_rotate(root.right)
return AVL_Tree._left_rotate(root)
return root
@staticmethod
def delete(root: TreeNode, key: int) -> TreeNode:
if not root:
raise KeyError
elif key < root.val:
root.left = AVL_Tree.delete(root.left, key)
elif key > root.val:
root.right = AVL_Tree.delete(root.right, key)
else:
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
else:
temp = AVL_Tree.get_min_value_node(root.right)
root.val = temp.val
root.right = AVL_Tree.delete(root.right, temp.val)
if root is None:
return root
root.height = 1 + max(
AVL_Tree.get_height(root.left), AVL_Tree.get_height(root.right))
balance = AVL_Tree.get_balance(root)
if balance > 1 and AVL_Tree.get_balance(root.left) >= 0:
return AVL_Tree._right_rotate(root)
if balance < -1 and AVL_Tree.get_balance(root.right) <= 0:
return AVL_Tree._left_rotate(root)
if balance > 1 and AVL_Tree.get_balance(root.left) < 0:
root.left = AVL_Tree._left_rotate(root.left)
return AVL_Tree._right_rotate(root)
if balance < -1 and AVL_Tree.get_balance(root.right) > 0:
root.right = AVL_Tree._right_rotate(root.right)
return AVL_Tree._left_rotate(root)
return root
@staticmethod
def get_height(root: TreeNode) -> int:
if not root:
return 0
return root.height
@staticmethod
def get_balance(root: TreeNode) -> int:
if not root:
return 0
return AVL_Tree.get_height(root.left) - AVL_Tree.get_height(root.right)
@staticmethod
def _left_rotate(z: TreeNode) -> TreeNode:
y = z.right
T2 = y.left
# Perform rotation
y.left = z
z.right = T2
# Update heights
z.height = 1 + max(
AVL_Tree.get_height(z.left), AVL_Tree.get_height(z.right))
y.height = 1 + max(
AVL_Tree.get_height(y.left), AVL_Tree.get_height(y.right))
# Return the new root
return y
@staticmethod
def _right_rotate(z: TreeNode) -> TreeNode:
y = z.left
T3 = y.right
# Perform rotation
y.right = z
z.left = T3
# Update heights
z.height = 1 + max(
AVL_Tree.get_height(z.left), AVL_Tree.get_height(z.right))
y.height = 1 + max(
AVL_Tree.get_height(y.left), AVL_Tree.get_height(y.right))
# Return the new root
return y
@staticmethod
def get_min_value_node(root: TreeNode) -> TreeNode:
if not root or not root.left:
return root
return AVL_Tree.get_min_value_node(root.left)
Red-Black Tree
 |
|---|
| An example of a red–black tree[3] |
In addition to the requirements imposed on a binary search tree the following must be satisfied by a red–black tree:[4]
- Each node is either red or black.
- The root is black. This rule is sometimes omitted. Since the root can always be changed from red to black, but not necessarily vice versa, this rule has little effect on analysis.
- All leaves (NIL) are black.
- If a node is red, then both its children are black.
- Every path from a given node to any of its descendant NIL nodes goes through the same number of black nodes.
Height difference tolerance: twice
| Algorithm | Average | Worst case |
|---|---|---|
| Space | ||
| Search | ||
| Insert | ||
| Delete |
2-3 Tree
B-tree
B+ Tree
Tests
Knuth, D. E. (1998). The art of computer programming: Volume 3: Sorting and Searching. Addison-Wesley Professional. ↩︎
Image is from https://www.javatpoint.com/avl-tree ↩︎
By Cburnett - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=1508398 ↩︎
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to algorithms. MIT press. ↩︎
