Cut Vertices and Bridges
A vertex in an undirected connected graph is an articulation point (or cut vertex) iff removing it (and edges through it) disconnects the graph. Articulation points represent vulnerabilities in a connected network – single points whose failure would split the network into 2 or more components. They are useful for designing reliable networks. [1] A graph is Biconnected iff it doesn't have cut vertex. biconnectivity is NOT transitive.
An edge in an undirected connected graph is a bridge iff removing it disconnects the graph. For a disconnected undirected graph, definition is similar, a bridge is an edge removing which increases number of disconnected components.
Like Articulation Points, bridges represent vulnerabilities in a connected network and are useful for designing reliable networks. [2] A graph is 2-edge-connected iff it doesn't have bridge. 2-edge-connectivity is transitive, i.e., if X, Y, and Z are three vertices in the graph, X is 2-edge-connected with Y, and Y is 2-edge-connected with Z, then X is 2-edge-connected with Z.
Both of these problems can be solved by Tarjan's algorithm. It only runs DFS once. For a graph represented by adjacency list, its worst-case time complexity is
Example
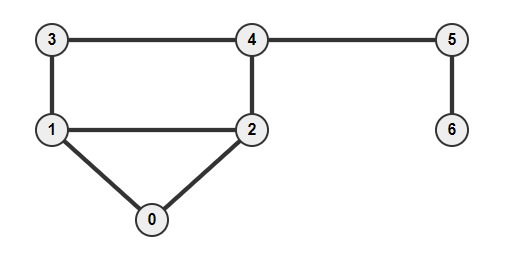
Adjacency List
- 0: 1 -> 2
- 1: 0 -> 2 -> 3
- 2: 0 -> 1 -> 4
- 3: 1 -> 4
- 4: 2 -> 3 -> 5
- 5: 4 -> 6
- 6: 5
Cut Vertices
from typing import List, Set
from collections import defaultdict
def cut_vertices(graph: List[List[int]]) -> Set[int]:
if not graph:
return set()
dfn = {}
low = {}
parent = defaultdict(lambda: None)
step = 0
ans = set()
def dfs(u):
nonlocal graph, dfn, low, parent, step, ans
dfn[u] = step
low[u] = step
step += 1
children_cnt = 0
for v in graph[u]:
if v not in dfn:
children_cnt += 1
parent[v] = u
dfs(v)
low[u] = min(low[u], low[v])
if parent[u] is None and children_cnt > 1:
ans.add(u)
if parent[u] is not None and low[v] >= dfn[u]:
ans.add(u)
elif v != parent[u]:
low[u] = min(low[u], dfn[v])
dfs(0)
return ans
Bridges
from typing import List, Tuple
from collections import defaultdict
def bridges(graph: List[List[int]]) -> List[Tuple[int]]:
if not graph:
return []
dfn = {}
low = {}
parent = defaultdict(lambda: None)
step = 0
ans = []
def dfs(u):
nonlocal graph, dfn, low, parent, step, ans
dfn[u] = step
low[u] = step
step += 1
for v in graph[u]:
if v not in dfn:
parent[v] = u
dfs(v)
low[u] = min(low[u], low[v])
if low[v] > dfn[u]:
ans.append((u, v))
elif v != parent[u]:
low[u] = min(low[u], dfn[v])
dfs(0)
return ans
